 Bild 12: Zusammenstellung mit (xy*xy) mod 140 und k=0.016 |
 Bild 13: wie Bild 12, aber mit (x*x+y*y)^2 mod 30 |
Chaos, Biologie und Fraktale
Teil5: Wirbel aus Interferenzen und die Locken in der Locke
Teil 5a
WIRBEL AUS INTERFERENZEN
Vorliegender Text bringt das Prismenspektrum mit der allgemeinen Wirbel-Erzeugung in Verbindung, spannt sozusagen den Regenbogen vom Hurrikan zum Proton. Ich halte diesen Teil meiner Arbeit für den wichtigsten, obwohl er nur am Rande mit Chaos und Biologie zu tun hat. Hier wird beschrieben, wie ein einzelner Wirbel entsteht, ganz gleich, ob in einem Lichtbündel oder in einer Flüssigkeitsströmung. Voraussetzung ist dabei Ordnungskraft durch Potential (oft in Form von Materie zu sehen). Dynamische Rückkopplungen, die Fraktale erzeugen, brauchen periodisch geordnete Randbedingungen. Sie sind leichter von der Natur zu realisieren, als man auf den ersten Blick denkt.
Schwebungen
Wellen können miteinander interferieren, wenn sie eine feste Phasenbeziehung zueinander haben. Gleiche Frequenz vorausgesetzt, können sich zwei Wellen mit gleicher Amplitude bei einer Phasendifferenz der halben Wellenlänge völlig auslöschen. Bei geringfügigem Frequenzunterschied erscheint die Auslöschung nur kurzzeitig wiederkehrend. Über das Interferenzbild läuft dann eine periodische Bewegung, die sogenannte Schwebung. Was geschieht, wenn der Frequenzunterschied nicht geringfügig bleibt, sondern schrittweise zunimmt ? Hört die Schwebung dann irgendwann wieder auf ? Werden über Bifurkationskaskaden chaotische Zustände erreicht ? Ein einfaches Computerexperiment kann die Antwort bringen: Wir addieren zwei reelle Wellen in einer Bildzeile. Das sind einfach zwei Cosinusfunktionen der Amplitude Eins, der Phase w* t, aber unterschiedlicher Kreisfrequenz w . (Abszisse ist t , Ordinate ist halbe Frequenzdifferenz m ) :
A=COS(w1 * t)+COS(w2 * t) (A1)
mit w1=1+m , w2=1-m , 0<m<1
Die Nullstellen (für Gesamtamplitude A um Null) werden mit einer anderen Farbe markiert als der Rest des Bildes. Sie ergeben im Bild zusammenhängende (dunkle) Linien, genauer gesagt, ein Netz aus zwei Hyperbelschaaren. Zusätzlich kann man die Lage der Extrema ( für A um +2 oder um -2 ) mit weiteren Farben anzeigen. Das Bild wird besonders einfach, wenn man den Frequenzunterschied der beiden Cosinuswellen symmetrisch zur Eins anwachsen läßt (A1), um den festen Mittelwert Eins zu erhalten, der im Bild seine Nullstellen als senkrechte Linien zeigt.

Bild1: Nullstellen-Netz von Gl.(A1) für bszisse 0<t<50 auf 300 Pixel. Die Ellipsen in den Netzmaschen zeigen die Lage der Maxima und Minima.
Die Cosinusfunktionen werden einfach in einer Zeile wie im Zeitablauf von links nach rechts abgerollt und sofort addiert, beginnend mit der untersten Zeile bei der halben Frequenzdifferenz m =0. Eine Zeile höher existiert bereits der erste Frequenzunterschied und irgendwo weit rechts, hier weit außerhalb des Bildes, erreicht die vorderste abfallende Hyperbel diese Zeile und markiert damit die Nullstelle der ersten Schwebung (halbe Wellenlänge). Die halbe Frequenzdifferenz m wächst mit jeder Zeile und erreicht am oberen Bildrand die Eins. Dadurch werden im Bild alle Frequenzverhältnisse von Eins bis Unendlich erfaßt, natürlich gerastert entsprechend der Zeilenzahl.
Die von oben nach rechts unten schräg einlaufenden Nullstellen gehören zu den Schwebungsfrequenzen w=(w1-w2)/2= m und sind somit bei jedem Schnittpunkt direkt an der Ordinate ablesbar. Benutzt man für obigen Ansatz die Additionstheoreme für Winkelfunktionen, ergibt sich (A2) mit den Nullstellen (A3).
A = 2* COS(t)* COS(m* t) (A2)
t1 = p * (0.5 + k1)
und
t2 = p/m * (0.5 + k2) (A3)
k1= 0,1,2,3... k2=
0,1,2,3...
Die Netzkreuzungen befinden sich bei (A4), d.h. bei allen Verhältnissen ungerader ganzer Zahlen, wobei die kleinere ungerade Zahl oben im Zähler steht.
für t1 = t2 :
m = ( 2* k2+1 ) / ( 2* k1+1 )
(A4)
k2 < k1
Jede Zeile, die auf einer solchen Netzkreuzung liegt, besitzt ein rationales Frequenzverhältniss w1/w2 und trifft in festem Rhythmus auf weitere Kreuzungen. Bildzeilen, die nie auf eine solche Netzkreuzung stoßen, weisen keine Periodizität auf, gehören zu irrationalen m. Dort kann man tatsächlich von einem chaotischen Ergebnis der Überlagerung sprechen. (Zu erwartende Bifurkationskaskaden müßten jeweils zwischen den m aus (A4) liegen. )
Jedoch liegen die Netzkreuzungen für wachsende t immer dichter und die Linien werden flacher und dünner (Zerfließen der Schwebung, Bilder 21 und 22), so daß sehr bald das Bildschirmraster die Linien unterbricht, überdeckt oder dort zusammenfügt, wo eigentlich keine Verbindung ist. Hier tritt der sogenannt Moire-Effekt auf (Bilder 2, 3, 20)
 Bild2: Der Moire-Effekt beginnt. Gerechnet wie Bild 1, mit 100<t<150 |
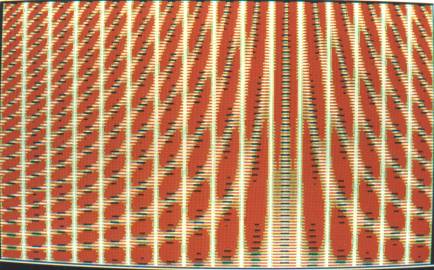 Bild 3: wie Bild 1, mit 200<t<250 |
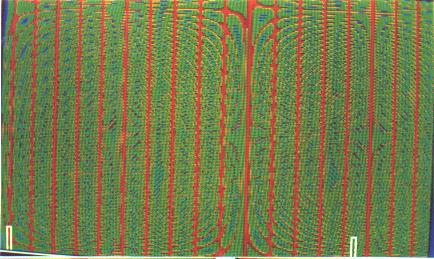 Bild 20: wie Bilder 1 bis 3, mit 0<t<1000 , markierte Ausschnitte sind Fenster für die Bilder 21(links) und 22(rechts) |
|
 Bild21: linkes Detail von Bild 20, 0<m<0.1, t-Breite=10; hier natürlich kein Moire-Effekt ! |
 Bild 22: wie Bild 21, rechtes Detail von Bild 20 |
Er bedeutet das Wirksamwerden der vom Bildschirmhersteller geometrisch festgelegten Pixel-Schrittweite. Es ist eine zusätzliche Frequenz, die mit den Wellenabbildungen des Bildes in optische Wechselwirkung tritt. Das Bildschirmgitter ist als dritte Überlagerungsfrequenz (pro Bildkoordinate) zu betrachten. Die Frequenz beträgt hier G=180 Zeilen pro Bild. Wieder zeigt sich:
Die Strukturbildung beginnt mit der unabhängigen dritten Größe.
Stellt man sich für t wirklich den Zeitablauf vor, dann erscheint das Symmetriebild rhythmisch wieder, weil nach doppelter Komprimierung wieder je zwei gerade t1-Linien hinter dem Bildraster verschwinden usw.usf. .
Jetzt spielt es keine Rolle mehr, ob zwischen zwei Wellen perfekte Schwebung oder Chaos existiert. Die dritte Welle erzeugt eine neue Struktur im Ganzen. In dieser Struktur kann nun eine eigene Dynamik einsetzen, wobei eine gewisse Abgrenzung von den erzeugenden Grundmustern auftritt.
Für ein in t komprimiertes Bild der Breite 0<t<2pG verschwinden die senkrechten Netzlinien genau hinter jeweils einer Pixelspalte, und alle waagerechten und senkrechten Moire-Strukturen schließen sich zu einem einzigen symmetrischen Muster zusammen.

Bilder 4 bis 6: Symmetriebild. Im Bildspeicher ist jeweils das gleiche
Bild, es wurden nur drei verschiedene Farbtabellen verwendet. Gerechnet wie
Bild 1, mit 0<t<2pi*G auf G mal G Pixel, wobei hier G=180
Modulo-Muster
Genau das Muster von Bild 6 fand ich in einem Handbuch für Computergrafik wieder, wo es ganz anders erzeugt wurde. Es handelt sich um die Modulo-Operation der Funktion f=x* y. Und das ist nun nicht verwunderlich, weil bei obiger Wellenüberlagerung ebenfalls eine Hyperbelschaar erzeugt wurde, die uns im Falle der richtigen Komprimierung genau die Einheitshyperbeln y=1/x lieferte. Man programmiert den Grauwert des Bildes als:
g = INT(2xy) mod m (A5)
für 0<x<d, 0<y<d, k=s=1 mit
g: Farbe des Pixels (x,y)
d: Bildgröße in x oder y
G: Pixel-Anzahl für jeweils x oder y
m: Modulo-Wert (Farbanzahl, oder Normwert
Eins)
s: allgem. Strukturfaktor
k: um (mod G) reduziertes s = periodische
Strukturgröße,
auch Ähnlichkeiten für (mod G/n)
n ganz
Der Moire-Effekt entsprach vollkommen der Modulo-Funktion. Ich untersuchte nun gezielter den Moire-Effekt und fand den Zusammenhang (A6) zwischen Bildgröße d für x oder y, der Strukturanzahl k und der benutzten Pixelanzahl G:
d2 = 0.5 * G * m * s (A6)
k = s mod G
 Bild 7: Symmetriebild nach (A5) und (A6), mit (2xy mod 30), d.h. m=30, G=180, mit s=91. Es ist identisch mit s=k=1 Hier neu gerechnet (kein FotoScan) mit s=1, G=450, m=15, wegen (A6) ist d=sqr(1/2*450*15) und weitere |
 Bild 7a: wie Bild 7; Zusammenstellung aus Bildern mit verschiedenen s=k=2,3,4,5,6,7,8 mit m=30, G=180 und nach (A6) dazugehörigem d=sqr(G*m*s/2) |
Unter Strukturanzahl k pro Koordinate verstehe ich die Anzahl der (in diesem Fall) walzenförmigen Einheiten, gezählt an der Bildkante. Mit (A5) und (A6) erhielt ich Bild 7 und 7a. Am günstigsten wählt man für m die Anzahl der nutzbaren Grafik-Grauwerte bzw. -Farben, so daß g die Grauwerte Null bis m-1 liefert. Für k kleiner als G/2 erhält man auf dem Bild k* k identische Strukturen. Ein s zwischen G/2 und G entspricht einer Strukturanzahl k=G-s.
 Bild 10: (x*x-y*y) mod 30 mit k=2 auf 180 Pixel, hier 300 Pixel waagerecht; in Bild 8 für k=1 |
 Bild 16: wie Bild 10, mit k=4 |
Benutzt man statt der Funktion F1=2xy die andere Funktion für gleichseitige Hyperbeln F2=x2-y2, entstehen ähnliche Bilder, die nur um 45 Grad gedreht sind (Bilder 10 und 16). Für F3=x2+y2 bilden sich konzentrische Kreise (Bilder 11 und 17).
 Bild 11: wie Bild 10, aber mit (x*x+y*y) mod 30 |
 Bild 17: wie Bild 11, Abszisse k=7, Ordinate k=3; siehe Listing 7; es sieht sehr bewegt aus im farbbewegten Präsentationsmodus |
Betrachten wir F1 und F2 als Komponenten der quadrierten komplexen Ebene z2=(x+iy)2, dann ergibt sich als Betrag von z2 genau F3. Es gilt der Pythagoras F32=F12+F22 . Deutet man F3 als die Intensität einer Welle, ist es die Intensität der komplexen Welle z , oder es entspricht F32 der Intensität der Welle w=z2.
Iw=z* z =r exp(i w)* r exp(-i w)=r2=x2+y2=F3=SQRT(F22+F12) (A7)
Alle drei Funktionen gehören zusammen. Die gleiche Welle z=x+iy (gemischte raumzeit) bedeutet im Fourierraum einen Punkt der Intensität F3, wobei die Frequenzgröße w beim Summieren verschwindet, jedoch über den Speicherort (Index w) verankert bleibt.
Nun möchte ich zur Wellenaddition (A1) zurückkehren, die nur die reelle Projektion einer Welle betrifft, aber bei passendem Zeitmaßstab gleichseitige Hyperbeln erzeugt, genau wie F1. Aus (A7) ist ersichtlich, daß F2 zu F1 orthogonal liegt und beide zwei verschiedene Projektionen der Gesamtwelle sind, deren Intensität durch F3 im Hologramm gespeichert wird. Auch der materielle Hologrammkristall speichert nur die Intensität, den skalaren Betrag der überlagerten Wellen. Nur indirekt, über den Ort der Intensitäts-Speicherung, wird die Phaseninformation (als reine Zeitgröße) abgelegt. Die materielle Speichersubstanz muß die dritte Welle liefern, sowohl bei Aufzeichnung als auch bei Wiedergabe, sonst geht es nicht. Deswegen wird am besten in Kristallen gespeichert (Gitterkonstante G) .
Welt als Pulsgeber
Was verbindet (A1) mit (A7) ? (A1) ist nach Frequenzen sortierte Strahlung, ist weißes Licht nach einer beliebigen Spektralzerlegung. Wir sehen an den Nullstellen der Schwebung die Inversion y=1/x. Damit entsteht spontan hyperbolische Geometrie, genau wie beim Quadrieren in der komplexen Zahlenebene. Daraus folgere ich wiederholt: Die Gaußebene entwickelt unter Quadrierung prismatische Eigenschaften, ist dadurch in jedem Kristall mehrfach physisch realisiert. Das Rotieren der unquadrierten Gaußebene z=x+iy zeigt an, daß man über das Wurzelziehen vom quadratischen Ursprung zur von uns verwendeten Normalform kommt. Quadrieren heißt demnach Nichtrotieren, heißt kristalliner Ursprung oder Rückkehr zum Ursprung. Quadrieren heißt Wirbel auflösen, Rotation anhalten, heißt Energie-Entzug.
Betrachten wir Drunvalos Schöpfungsablauf (Teil 3), erkennen wir: Die männliche kristalline Urform ist quadratisch. Durch Wurzelziehen kam die weibliche rotierende Kugelform in die Welt. Wurzelziehen heißt Rotation in Gang setzen. Wurzeln sind mehrdeutig und periodisch, wie beim Drehen und Schwingen.
Bekanntlich bildet eine komplexe Zahl allein schon Schwingung oder Welle ab. Kristalle sind periodische Strukturen, sozusagen eingefrorene Wellen, die natürlich auch als Straßen und Spiegel für fremde Wellen zur Verfügung stehen. Gleichzeitig gilt für ein kontinuierliches Lichtspektrum die Gleichung (A3) und es bleibt übrig: Kristalle invertieren, weil sie ordnen. Es sind die äußeren und inneren Spiegelungen an den Kugelflächen der Flower of Life. Auch jede Zentrifuge ordnet durch Fliehkraft. Ebenso sortieren der Wind und das Meer ihre leichten und schweren "Passagiere". Dort wirkt auch Trägheit trennend, aber wesentlich die Gravitation. Wenn etwas Invertiertes wieder invertiert wird, pulsiert es. Um beim Licht zu bleiben: Prisma und Linse bringen durch ihre ordnende Kraft den Rückweg von der runden weiblichen Welle zur männlichen Inversion, vom Bogen zur Gerade und umgekehrt.
Die Apfelmännchen-Iteration übergibt das quadrierte z, nach vorheriger C-Addition allerdings, wieder dem einfachen z. Das ist im Grunde Wurzelziehen und erneut die Rotation anschieben. Die Durchführung der Funktion z2 stoppt die Rotation und zeigt kurzzeitig die ruhenden Hyperbeln der Inversion. Man kann es mit dem maximalen Pendelausschlag vergleichen, wo einen Moment lang die Bewegung stillsteht, weil sie die Richtung ändert. Die dazwischengeschaltete C-Addition entspricht der Erdbeschleunigung oder der Fadenspannung bei einer Drehschwingung. Beim nächsten z2 wird wieder aller Energiezuschuß bis hin zur Null-Geschwindigkeit verbraucht. Das Apfelmännchen ist ein ständiges Pendeln zwischen männlich und weiblich, wobei die konstante Größe der Energieabsorption +C jedes Taktes über die Lebensfähigkeit (Stabilität) des Vorganges entscheidet. Nur in einer dünnen Schicht der Apfelmännchen-Oberfläche geschehen alle dynamischen Kreisläufe, wie auch die Wunder des Lebens auf der Oberfläche unseres Planeten.
Weißes Licht
Die Hyperbeln t2 in (A3) mit t=C/m bilden im Dreidimensionalen jeweils einen hyperbolischen Kegel (s.Wolfgang Wiedergut), hier als die Schwebungs-Nullstellen eines parallelen Lichtflusses aller Frequenzen, also von total weißem Licht. Für den Kegel legt man nicht alle Perioden nacheinander auf die Zeitachse. Es genügt die ortsfeste Abbildung einer Schwebungs-Periode bzw. der ersten Hyperbel als Ereignis an einem Punkt P, an dem Streulicht in alle Richtungen auftritt. Die t-Achse wird nun r-Achse genannt und rotiert um Achse m für Streulicht im Nullpunkt P.
Dieser Kegel des weißen Lichtes dehnt sich mit jeder Schwebungsschwingung aus, verbreitert sich. Für jede Schwebungswelle (nächste k2-Hyperbel) existiert von ihm eine neue "Zwiebelschale" mit m-abhängiger Dicke in Richtung r. Sie werden jedoch schnell sehr dünn und fließen zusammen.
Da Licht elliptisch-transversal schwingt, liegt die Schwingungsrichtung parallel zur Kegelhauptachse, also longitudinal zum Kegel. Das heißt, wenn die Kegelspitze die Wellenausbreitungsrichtung der Schwebungswelle anzeigt, verkörpert der Kegel dort eine Schallschwingung. Er selbst sieht auch aus wie eine Röhre, die Schall fortleitet. Und da wir den Koordinatenmaßstab im natürlichen Frequenzraum nicht kennen, könnten diese Röhren u.U. auch sehr lang sein (exponentieller Maßstab). Beim Gegenteil, dem doppelt-logarithmischen Maßstab, wird die Hyperbel zur geneigten Gerade und das Ergebnis ist ein richtiger Kegel, den auch das rotierende Sterntetraeder erzeugen könnte ...
Zusammenfassung: Weißes Licht wird hinter dem Prisma (oder im abstrakten Frequenzraum) von Schall begleitet. Auch Schall (weißes Rauschen) kann im Frequenzraum transversal werden, und damit lichtartig. Umgekehrt entsteigt dem Licht des Frequenzraumes für uns ein Ton, und aus dem dortigen "Wort" wird hier Licht.
Strömung und Wirbel
Man kann (A2) gleichzeitig als eine Strömung in Richtung t ansehen, wobei ein Geschwindigkeitsgradient senkrecht zur Fließrichtung anwächst (F2=v, F1=dv/dx). Zwischen den fließenden Schichten müssen Mikroturbulenzen entstehen, die ein zu den Bildpixeln analoges Grundgitter darstellen. Bei bestimmten kritischen Werten können sich dann große stabile Wirbelstrukturen (nach (A6)) ausbilden. Der Vorgang im Einzelnen:
Die Größe m in Bild 1 wäre dann der Geschwindigkeitsbetrag, unten Null und oben maximal, wie vom Rand bis zur Mitte eines Flusses. Die Strömung fließt von links nach rechts. Unten ist das Ufer, oben die Flußmitte. Für m nach (A4), den sauberen Schwebungszuständen, wird die Strömung laminar fließen, weil dort Periodizität herrscht (De-Broglie-Welle). Das betrifft wegen der Kohäsion auch die nächste Umgebung. Es bildet sich eine zusammenhängende Schicht annähernd gleicher Geschwindigkeit. Aber zwischen zwei Schichten müssen sich verschiedene (zum Teil gemittelte) Periodizitäten angleichen, dort wirkt dann der Geschwindigkeitsgradient als Kraft senkrecht zur Bewegung. Dadurch entstehen Mikroturbulenzen zwischen den Schichten. Man kann auch sagen: Durch Mikro-Reibungsschichten entsteht Viskosität. Die Tatsache, daß in jeder Strömung mit Geschwindigkeitsgefälle mathematisch vorgegebene Schichten entstehen müssen (um die Netzkreuzungen herum - siehe (A4) ), ist allein schon interessant. Die voneinander getrennten Laminarschichten entsprechen der Gitterkonstante im Kristall. Dadurch wird die Strömung (bzw. der Wirbel) "hologrammierbar", wird zu einem möglichen Informationsspeicher. Es geht hier ganz allgemein um Flüssigkeiten. Bei Wasser kommen besondere Struktureigenschaften hinzu.
Der dazugehörige hyperbolische Kegel liegt senkrecht zur Strömung, ab der Mitte gespiegelt wie eine Brücke, die sich in der Mitte verengt. Die beiden Kegelspitzen sind aufeinander zu gerichtet. Der Effekt bleibt im Wasser. Diese orthogonale Kraft wirkt zur Mitte hin. Schwimmer und Taucher kennen das.
Da bei Abbildung 0<t<tmax für (A2) der mittlere Gradient proportional tmax ist, also von der t-Komprimierung des Bildes abhängt, müssen mit steigendem Gradienten die Laminarschichten immer dünner werden und die Zahl der Reibungsschichten mit Mikroturbulenzen nimmt zu. Das ist gut sichtbar am Bild 1. Von oben her geraten mit t neue Linien ins Bild, und bei 2t verdoppelt sich ihre Anzahl. Die Menge und Dicke dieser Störschichten erreicht schließlich einen kritischen Wert und zerstört die Laminarstruktur (kritische Reynoldzahl).
Bei einem so starken Geschwindigkeitsgradienten, der dem Symmetriebild (Bild 4) entspricht, existiert die parallele Schichtenstruktur plötzlich nicht mehr. Alle Mikroturbulenzen füllen den Raum aus und jedes Flüssigkeitsteilchen findet als vektorielles Ergebnis der umgebenden Kräfte eine gekrümmte Bahn. Innerhalb dieser gekrümmten Bahnen werden sich wieder laminare Schichten ausbilden. Es entstehen jetzt sehr große Wirbel, im Vergleich zu den Mikrowirbeln. Nun hat die Flüssigkeit ihren Energieinhalt dichter gespeichert. Die Reynoldzahl sinkt für die nun gekrümmte Bahn wieder in unterkritische Bereiche ab. So bleibt sie stabil und das neu entstandene Gebilde wird selbständig. Die inneren Teilchen überholen immer die Äußeren im Wirbel (Impulserhaltung). Das gibt einen "Auftrieb" nach innen, bis die Zentrifugalkraft das Gleichgewicht hält. Jede weitere Kraft, z.B. aus einem Schallfeld, verändert die Schichtenstruktur. Ähnlich, wie auf den Preisschildern für elektronische Registrierkassen, steckt Information in den verschieden dicken Flußlinien. Der Wirbel ist eine Schallplatte. Er wird auch ein spezifisches Rauschen abgeben und damit das ursprüngliche Schallfeld kopieren und mit sich selbst rückkoppeln. So kann auch die homöopatische Information lange im Wasser bleiben. Das Verschütteln gibt Energie für neue Wirbel - das sind sozusagen die weißen Blätter zum sofortigen Beschreiben.
Hat sich die ursprüngliche Strömung zum großen Wirbel umgeformt, haben sich die beiden Kegel, wie beim Durchbrechen einer Brücke, vereinigt und sind nach unten gerichtet. Auch dies begegnet den Schwimmern im Fluß.
Natürlich ist in Bild 4 nichts mit Fliehkraft und Zähigkeit programmiert. Im Grunde wurden nur zwei harmonische Wellen und eine Rechteckwelle additiv verknüpft, auch in (A6) mit den Frequenzen k und G (Einheit 1/Bild) und der "Wellenlänge" m . Auch ergibt sich in der Computergrafik kein typischer Wirbel, weil das kartesische Bildschirmraster (Rechteckwelle) in der Natur nicht vorkommt, eher Kreisemuster (siehe Heilige Geometrie in Teil 3).
Das Strömungsbeispiel zeigt uns, daß die Wirbelerzeugung nur für Licht und andere Wellen das Prisma benötigt. In der Natur wirken überall Potentialdifferenzen, wie Höhenunterschiede, dank der Gravitation. Desweiteren greifen Sonnenerwärmung, elektrische Aufladung und Trägheitskräfte jeder Art ebenso ordnend ein wie die Prismen, wenn eine gewisse Regelmäßigkeit zugelassen wird. Der Einfluß unregelmäßiger Störungen muß begrenzt bleiben. Die Systeme brauchen Abrenzungen zum Schutz ihrer Ordnung.
Eine Flüssigkeit oder ein Gas, in Bewegung durch ein sauberes Potential, sortiert eigentlich von selbst seine Bestandteile nach Größe, Masse oder anderen Kriterien, bis auch dort Harmonie einkehrt, d.h. bis der Gradient ein kontinuierlicher ist. Dabei oder danach besteht die Chance, große Wirbel zu bilden. Existieren schon zu viele kleine Wirbel, die nicht physisch herauswandern können, müssen sie in Konkurrenz treten und Abgrenzungsmuster bilden, die auch zeitlich variabel sein können, wie bei der Wirbelschleppe hinter einem umströmten Hindernis. Gleichsinnige Wirbel vereinigen sich bei der Berührung und werden somit größer. Gegensinnige löschen sich aus. Es bleiben also Fraktale übrig aus rechtsdrehenden und linksdrehenden Wirbeln und ihren Zwischenräumen, den Nullgebieten nach Auslöschung. Das Apfelmännchen ist solch eine fraktal zerrissene Null zwischen +i Unendlich und -i Unendlich.
Alle neu entstandenen Wirbel sind Träger von Energie (Kraft) in neue Richtungen hinein, die orthogonal zur alten Fließrichtung stehen. Auch das Pointing-Kreuzprodukt ist nichts anderes.
Hier wird angedeutet, wie man alle Kräfte und andere physikalische Größen auf Wellenparameter zurückführen und damit normieren könnte (sehr hypothetisch).