.

Chaos, Biologie und Fraktale

Teil 3: Computertiere, Goldener Schnitt und Hyperkomplexes
(Veröffentlichung 1996)

Teil 3a

COMPUTERTIERE

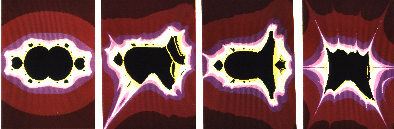...................Bild 1 bis 4

Mutation

Ein Tipp-Fehler beim Programmieren der Iterationsgleichung wirkt sich am Bild wie eine Mutation aus. Die Bilder oben zeigen eine Mutation von Z_n+1=Z_n³+C (Bild 1, ganz links)., wobei beim Ausmultiplizieren jeweils ein Fehler gemacht wurde. Ein innerer Faktor y war zum Beispiel aus der Kette (A1) verloren gegangen (Bild 2):

..................X = xxx - xyy - xyy - xyy + C_x

aus ..........Y = - yyy + xxy + xxy + xxy + C_y .....................................................(A1)

wurde ......Y = - yy ..+ xxy + xxy + xxy + C_y

Die Fühler und Krallen sind schon "tierischer" geworden, man sieht aber noch die Verwandtschaft mit Bild 1. Die Bilder 3 und 4 sind weitere Mutationen. Auch hier ist es wie in der Biologie: Durch Informationszerstörung kommt es zu Krüppeln und Monstern, wohl kaum zur Höherentwicklung (Irrtum des Darwinismus).

Die komplexe Zahlendarstellung wird durch Tippfehler verletzt. Zwar verlieren die Bilder dann ihre Symmetrie, können aber dadurch interessantere Versionen der Computerwelt werden. Auch der Ansatz (A4) im nächsten Abschnitt beruht auf Nicht-Komplexen Eingriffen und führt trotzdem zu einem insektenähnlichen "Tier". Daraus ist zu folgern, daß die komplexe Wellendarstellung nur den harmonische Spezialfall beschreibt, während im allgemeinen die Iterationen sowieso ein anharmonisches Wellenprofil erzeugen. Erst die Zyklus-Welle am Ende der Iteration, als nun übergeordneter stabiler Schwebunggszustand, paßt wieder zu unserem bescheidenen Wissen über Wellen und Bewegungen. In diesem Sinne muß der Begriff Interferenz weiter gefaßt werden: Überlagerung von nichtlinearen und rückgekoppelten Prozessen, die im stabilen Fall Wellen bilden, darunter fallen auch Fraktale als "verallgemeinerte Wellen".

Verkoppelte Gleichungen und Ketten

So, wie sich die Komponenten x und y bei komplexen Elementarfunktionen miteinander vermischen, so kann man auch im Komplexen verschiedene Gleichungen miteinander verbinden. Der Kontrollparameter C könnte eine vorgegebene Zeitfunktion (Umwelteinfluß) sein, oder hauptsächlich über ein Nachbarobjekt, wie etwa die gleiche Nachbarzelle im Zellverband, gesteuert werden. Dieses Modell der wechselwirkenden Kopplung identischer Zwillinge wurde für einige Fälle untersucht.

In den Bildern von Explosion wurde ein Apfelmännchen mit einem anderen verkoppelt (Zwillingsverfahren) über die Gleichung (A2) mit (A3) oder (A4).

Z1_n+1 = Z1_n² + C1 ; Z2_n+1 = Z2_n² + C2 ......................................(A2)

mit C1 = C (1+ a* Z2) ; C2 = C (1- a* Z1) ............................  ........(A3)

oder mit

C1 = C_x(1+ a* Z2_x) + i (C_y *(1 - a* Z2_y) ;
C2 = C_x(1+ a* Z1_x) + i (C_y* (1 - a* Z1_y)                                           (A4)

wobei wie immer C = C_x+ i* C_y ; Z = Z_x+ i* Z_y

Der Einfluß des jeweils anderen Apfelmännchens zeigt sich in einer additiven Zusatzgröße, in die multiplikativ C selbst und ein Steuerparameter a (Kopplungsfaktor) eingeht. Es erwies sich als günstig, für eines der beiden Apfelmännchen das Vorzeichen der Koppelgröße zu wechseln. Dadurch geschieht die Übergabe in einer festgelegten Fließrichtung. In (A4) ist die Verkopplung so assymmetrisch, daß sogar der komplexe Zusammenhang nicht mehr gegeben ist.

In jedem Falle beobachtet man Veränderungen des Fraktals. Läßt man die Kopplungsstärke a für ein Bild fest und macht eine Reihe von Bildern mit wachsendem a , dann wirkt a wie ein Evolutionsfaktor: Das Apfelmännchen macht eine Entwicklung durch: Es schiebt seine Kugeln von sich, die sich danach in fortwährender Teilung auflösen. Der Hauptkörper schrumpft und deformiert. Eine Divergenzinsel im Hauptkörper bildet sich in Randnähe, die wie ein Auge aussieht und langsam nach außen zum übrigen Divergenzbereich wandert. Bei komplexem a bekommt das "Tier" zeitweilig "Füße" oder einen "dicken Schwanz" (Bild_Kaulquappe) . Bild_Wappen ist ein kleines Detail bei a=0,75 .

Ähnlich behandelt, entwickelt die Gleichung (aus Vierpol-Theorie)

Z_n+1 = ( Z_n + C ) / ( 1 + C* Z_n^k )                    mit k=3 .................... ....................(A5)

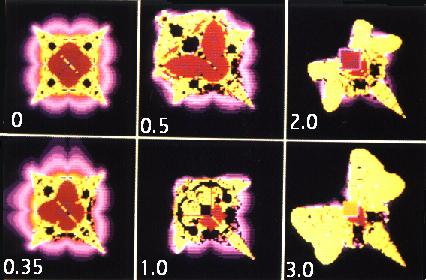
aus einem Stern einen kopflosen Schmetterling, oder bildet insektenähnliche Inseln, die sowohl von oben als auch von oben-links-diagonal auf dem Hauptkörper "einlanden"(bei steigendem Parameter a).

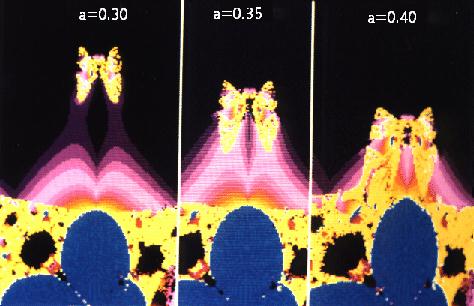
Diese Chaos-Inseln liegen für a=0 als Punkt im Unendlichen, nähern sich der Null mit a^-2 , wachsen dabei und vereinigen sich schließlich mit dem Hauptkörper bei etwa a=0.4 . Das sieht aus, als ob ein geflügelter Engel (Bild Engel1 oder Engel2 oder Engel3 - ist oben im linken Bild von Landung3) landet, oder an der Spitze ein Hütchen bildet. Bei dieser Vereinigung wölbt sich das Landegebiet den Neulingen freudig entgegen (s.Bild Landung2), sieht danach aber dick und gespenstig aus (s. oben erstes Bild). Die Zahl der Iterationen läßt während der Annäherung ein wachsendes "Kraftfeld" erkennen. Die Vereinigung einer Chaosinsel mit dem Hauptkörper ist vermutlich dasselbe Phänomen wie die Vereinigung getrennter Chaosbänder jenseits der Chaoskante, was wiederum einem nichtlinearen Verhalten höherer Ordnung entspricht. Das Verfolgen der Variable an einigen ausgewählten Punkten (Attraktordarstellung) dürfte für jeden Chaos-Theoretiker ein großes Vergnügen sein.

Für andere k in (A5) entstehen ebenfalls sternförmige Fraktale, die sich im Zwillingsverfahren auch zu vielfältigen Computertieren umformen lassen .

Ich denke, man sieht an solchen Beispielen, daß die im Computer leichter durchschaubaren Vorgänge durchaus allgemeine Rückschlüsse auf biologische Systeme zulassen, da sich hier wie dort vielfältige Rückkopplungen und Schwingungen kombinieren.

Kausalität in nichtlinearer Welt ?

Definiert man Linearität als proportionalen Zusammenhang zwischen Ursache und Wirkung, dann können reale physikalische Prozesse genaugenommen nicht linear sein. Unser Raum ist dreidimensional und nicht eindimensional, wie es eine im zeitlichen Nacheinander verkoppelte lineare Ursache-Wirkungskette vorschreibt. Es kann ein großer Unterschied sein, ob ein räumlich angrenzender, parallel verlaufender Prozeß haargenau synchron verläuft oder nicht. Problemlos beherrschbar sind nur die beiden Extremfälle von sequentieller und serieller Kausalität. Unter sequentieller Kausalität ist das bekannte kettenförmige zeitliche Aufeinanderfolgen von Ursache und Wirkung gemeint, unter serieller Kausalität ein ganzer Schwarm von einzelnen Kausalketten, die verkoppelt parallel laufen und absolut synchron getaktet sind, sodaß die Kausalität für die größere Einheit wieder sequentiell wird. Aber interessant - und nichtlinear - wird es bei Abweichungen von diesen Extrema (/Augustin/).

Auch der NEWTONsche Kraftbegriff braucht die lineare Kausalkette. Für die mathematische Beherrschung von Kraftfeldern müssen entweder ideale Symmetrien vorliegen oder man behilft sich mit lokalen Näherungsmethoden, d.h. man iteriert bereits, aber auf der Basis von Linearisierungen.

Eine ideale Symmetrie erlaubt die eindeutige Lösung. Sie betrifft den Gleichgewichtsfall, auch für Schwingungen - hier liegt dynamisches Gleichgewicht vor. Ist die Symmetrie gebrochen, kann zusätzliche Information in anderen Raumrichtungen stecken als den ursprünglich kausal hervorgehobenen. Energie wird immer quantisiert übertragen, so daß der Extremfall echter Synchronizität unglaublich wäre. Und doch stellt sie sich ein durch den periodischen Attraktor in der Rückkopplung. Man denke an den Laser oder den Frequenz-Mitnahmeeffekt in elektrischen Netzen. Das System reagiert dann als Ganzheit und bekommt die neue Eigenschaft der Abwärtsverursachung, einer nach innen gerichteten Kausalität.

Hat diese (oft ungezielte) zusätzliche Querketten-Information eine Wirkung ? Ja, sie kanalisiert neue Kausalketten. Für Newtonsch` erfolgreiche Anwendungsbereiche kompensieren sich diese Querketten - oft als Folge von Rückkopplungen -, dann sind Kräfte als Vektoren überlagerbar. Das gilt für nahezu lineare Verhältnisse, aber nie in Verbindung mit schnellen Bewegungen, weil dann die Wahl des Überlagerungszeitpunktes auf das Ergebnis Einfluß nimmt. Wenn sich die zufälligen Querketten nicht kompensieren, bildet sich eine Struktur durch eine netzartige nichtlineare Kraft. Ein Muskelsystem z.B. ist so aufgebaut, daß es optimal Kräfte kanalisieren kann (/Augustin/). Es kommen zwar alle benötigten Muskeln zum Einsatz, aber weder gleichzeitig noch nacheinander. Im ersten Fall würde die Bewegung einer Explosion gleichkommen und der Verschleiß wäre zu hoch, im zweiten Fall wäre die Aktion fast wirkungslos. Die Optimierung erfolgt so, daß sich eine zusätzliche Welle ergibt, weil ein vom Körperbau vorgegebener Verzögerungsvorgang abläuft. Die zusätzliche Welle besitzt keine Energie, sie entsteht aus Information, kodiert im Körperbau, und übt doch Wirkung aus. Sie kanalisiert Kausales mit Parallelem, verbindet Raum und Zeit.

In der Natur entstandene Fraktale sind höchst unregelmäßige, bizarre Gebilde, weit entfernt von wirklicher Symmetrie. Diese Erscheinung versperrt störenden kausalen Querketten innerhalb der Struktur den Weg, leitet anfänglich falsche Energieflüsse um und um, und läßt sie nicht entweichen. Nur gezielt offengelassene Kanäle bleiben übrig (Bild_Julia). Hier wird durch die fraktale Strukturierung eine neue Nichtlinearität aufgebaut, um zufällige Nichtlinearität zu bekämpfen. Die Natur nutzt den Symmetriebruch als Mittel der Stabilisierung. Symmetrisches kann die Symmetrie verlieren, kann unbrauchbar werden, wenn die Funktion ausschließlich auf der Symmetrie beruhte. Unsere Physik der Linearität schreckt vor biologischen Systemen zurück, aus gutem Grund: Es herrscht Werkzeugmangel für Nichtlineares. Sie wagt sich höchstens an ideale Kristalle heran. Aber beide Strukturarten haben periodisches Verhalten als Gemeinsamkeit. Eine Störung im Kristall hat mit Sicherheit größere Folgen für seine Schwingung, als eine gleich große Störung im fraktalen Biosystem. Die Physik muß flexibler werden, wenn sie die Mechanismen des multikausalen Prozeßverhaltens verstehen will.

Kondensierte Freiheitsgrade

Nehmen wir einmal an, der hypothetische Urknall, die "Geburt" unseres Kosmos, habe wirklich stattgefunden. Ich habe da zwar starke Zweifel, aber die Frage wird oft erörtert. Was "vor" dem Urknall war, ist undiskutabel. Schon das Wort "vor" ist unzulässig, weil mit dem Anfang zusammen erst die Zeit geboren wurde. Aber für die Zeit "kurz danach" gibt es gewisse Befunde, z.B. die kosmische Hintergrundstrahlung. Sie weist darauf hin, daß es damals sehr heiß war. Und zwar so heiß, daß nur Strahlung existieren konnte. Kein Elementarteilchen als solches konnte vorhanden sein.

Da es nun heute nicht mehr so heiß ist, muß es eine Abkühlung gegeben haben, z.B. aufgrund der Expansion des Kosmos. Wegen der Abkühlung konnten Teilchen entstehen, d.h. aus der Strahlung kondensieren, wie die Schneekristalle an Staubkeimen in kühler feuchter Atmosphäre. Soweit die übliche Erklärung in der Physik, die meine Hypothesen aus Teil 1 und 2 nicht berührt. Man kann es aber auch andersherum sehen:

Die Kondensation begann zuerst, weil Kondensation ein Entwicklungsvorgang ist. Kondensation nicht als Folge der Abkühlung, sondern irgendwie anders angeregt (gezielt geistig). Die Teilchen hatten nun Masse. Wenn diese mit hoher Geschwindigkeit zum Zentrum ‘nach innen’ stürzen sollte, kommt es zu einer relativen Expansion des Kosmos und überhaupt erst zur Realität von Raum und Zeit. Hier ist Expansion und Abkühlung eine Folge der Kondensation.

Sind zwei Teilchen miteinander in Wechselwirkung (Bindung), legen sie eine Richtung fest, z.B. eine Achse, um die ein drittes Teilchen rotieren kann, wenn es sich zu den beiden gesellt. Das heißt, aus drei Teilchen kann aus der ebenen Dreiecksfigur ein Rotationskörper werden. Ein räumlich ausgedehnter Körper als neue Einheit ist dann entstanden. Er braucht zu seiner statischen Erfassung in einem Koordinatensystem schon sechs Komponenten: drei für die Position des Schwerpunktes und drei für einen zweiten Punkt, der eine markierte Richtung festlegt. Der zweite Punkt kann auch durch drei Orientierungswinkel ersetzt werden, es bleiben sechs Zahlen. Den gleichen Zahlensatz braucht man zusätzlich für Geschwindigkeiten, Beschleunigungen usw.. Aus vielen einzelnen dreidimensionalen Größen ist beim Zusammenfügen für den Körper je eine sechsdimensionale Größe geworden.

Gebundene Bewegung erzeugt Strukturen. Nichts geht verloren. Die vielen Freiheitsgrade der Einzelteilchen werden für den Aufbau der stabilen Form verbraucht. Formbildung (Morphogenese) entspricht kondensierten Freiheitsgraden. Die weitere Kombination von Struktur und Bewegung trennt vorher Ununterscheidbares und baut etwas Komplexeres auf, das in sich gebunden ist, das einen höheren Ordnungszustand darstellt. Da im Kondensat Unmengen von Freiheitsgraden der ehemaligen Bewegung fehlen und jetzt in der Bindungsenergie stecken, kann durch eine Temperaturmessung nur ein Absinken der Wärme festgestellt werden.

Geometrisches Gedächtnis in der Form

Kombiniert man verschiedene Strukturen oder verschiedene Bewegungen zu einem neuen Ganzen, dann lassen sich die Ergebnisdrehwinkel im allgemeinen nicht mehr in die Einzelkomponenten des Koordinatensystems zerlegen. Die zeitliche Reihenfolge ist wichtig geworden, in der die Montage stattfand. Man würde wichtige Zusammenhänge zerstören, versuchte man am lebenden System den Endzustand in einem Schritt zu erreichen. Der einfache lineare, der wieder zerlegbare Zusammenhang wird schon ab wenigen Kondensationsschritten unrealistisch. Soll der Vorgang wiederholt werden, muß die zeitliche Reihenfolge Beachtung finden. Siehe Beispiel Zellteilung. In diesem Stadium wird die Kondensation üblicherweise Evolution genannt. Wir wollen diesen Vorgang aber weiterhin Kondensation nennen. Man erkennt jetzt, warum Abkürzungen in der Embryogenese nie stattfinden. Der gesamte Weg muß wie beim ersten Mal immer wieder durchlaufen werden, aus geometrischen Gründen! Die identische Wiederholung des Ablaufes beim Wiederaufbau einer Struktur braucht ein Gedächtnis für die Reihenfolge. (Der gesamte Vorgang wird so wieder eine Rekursion.) Ursache ist unsere unsymmetrische Geometrie in Bezug auf Drehungen. Vermutlich hat das mit der allgemeinen Rotation des Kosmos zu tun. Ich erinnere an den "Ladungswind", der am Äquator der Riemannschen Zahlenkugel weht (BildW).
Und man kann kanuartige Schiffchen einer fest vorgeschriebenen Form bauen, die im Gegenuhrzeigersinn lange rotieren, wenn man sie anschiebt wie ein gekochtes Ei, aber im Uhrzeigersinn erst zu hüpfen beginnen, dann anhalten und umdrehen (/Drunvalo/). Es besteht in unserer Welt eine eindeutige Asymmetrie bezüglich der Drehungen.

Bio-Kondensation

Beim Biosystem angelangt, bemerken wir, daß hier nicht von thermodynamischem Gleichgewicht die Rede sein kann. Begriffe wie Abkühlung und Kondensation ordnen wir normalerweise nur den (angeblich) toten Dingen zu, wie z.B. dem Schneekristall. Wenn statische Gleichgewichte auf tiefster Ebene ebenfalls dynamische Gleichgewichte darstellen, sollte man die Betrachtung erweitern. Der Unterschied ist nur, daß dem Biosystem zusätzliche Energie zufließt, weil es zur Eigenbewegung fähig ist und schon durch die Pumpvorgänge an den Membranen und in den Kapillaren Arbeit leistet. Der Schneekristall entstand durch Energieabgabe, ein Vorgang, für den auch jedes gespeicherte ATP-Molekül bestimmt ist. Der sensorisch gesteuerte Wechsel von Sol- und Gelzustand des Zytoplasmas zeigt, wie empfindlich das Biosystem an Phasenübergänge gebunden ist. Der Organismus schwebt förmlich zwischen fest und flüssig. Er hat sich dynamisch eingeschwungen, wie ein elektrischer Schwingkreis des Radioempfängers. Die Frequenz des Schwingkreises ist genauso konstant wie der thermodynamische Zustand des Schneekristalls. Und wenn man sowohl die Zunahme der Komplexität (Organismus als Einheit), als auch den Verlust an Freiheitsgraden der atomaren und molekularen "Einzelteile" in Betracht zieht, ist die Biosynthese auf jeden Fall eine Kondensation.

Und doch bleibt ein Unterschied: Wo kinetische Bewegung vorliegt, wird mehr Energie gespeichert, auch bei niedrigen Umgebungstemperaturen. In der Schneeflocke ist zwischen den gebundenen Wassermolekülen auch Rückkopplung vorhanden, aber diese hat in jeder Kristallisationsphase zum gleichen Fixpunkt geführt, so daß am Ende das selbstähnliche Fraktal ohne zusätzliche Energiereserven daliegt und kein wesentliches zeitliches Verhalten zeigen kann. Im Biosystem sind Rückkopplungen im Gang, die zyklische oder stabile deterministisch-chaotische Lösungen erlauben - und damit Bewegungen, Veränderungen (auch der Rückkopplungsparameter), Wachstum. Kurz: breite Möglichkeiten zur Veränderung, die eben nicht nur von Wind und Wetter abhängen, wie bei der Schneeflocke.

Kosmische Pulsation ?

Im Gegensatz zur anorganischen Anhäufung "klumpen" Atome und Moleküle im Biosystem auf besonders geordnete und idividuelle Weise zusammen. Für die Biosynthese könnte man auch folgende mathematische Ausdrucksweise benutzen: Die Iterationsgleichungen der Zelle bleiben immer zusammenhängend, auch nach der Zellteilung, so daß die neu eingebauten Stoffwechselprodukte in feste Muster der Verkopplung mit einbezogen werden. Der ganze Körper bildet von Anfang an ein zusammenhängendes iteratives Gleichungssystem, ein Riesenmolekül.

Die Freiheitsgrade sind nicht nur zu Form, sondern auch zu Masse kondensiert. Alle gebundenen Zustände, die weniger Gesamtenergie besitzen als einzeln, haben eine geringere Gesamtmasse als vor der Bindung. Die Bindungsenergie wird in diesem Fall in Form von Strahlung abgegeben, anschließend ‘fehlt‘ Masse. Denkt man diesen Ablauf konsequent zu Ende, ergibt sich eine kosmische Pulsation: Schließlich würden irgendwann Raum und Zeit wieder schrumpfen, der Strahlungsanteil wieder zunehmen. Es müßte dann die Temperatur ansteigen trotz (oder wegen) der Kondensation! Das heißt: Die konsequent fortschreitende Kondensation ist mit Ihrem Gegenteil, dem "Verdampfen" der Materie verbunden. Ist unsere Biostrahlung eine notwendige Folge ständigen Kondensierens? Möglicherweise nicht. Aber wenn doch, bleibt uns die heikle Frage: Was überwiegt? Erzeugen wir eine besondere Raumzeit, weil wir Materie anziehen (verbauen, kondensieren) oder bauen wir Raumzeit durch Verstrahlung von Bio-Energie ab? Wer sind die größten, die ausschlaggebenden Kondensierer und Strahler unseres Universums? Wesen wie Menschen, Planeten, Sonnen, Galaxienkerne oder Quasare?

Irrationales

Betrachten wir die scheinbar regellose Anordnung der Primzahlen auf dem Zahlenstrahl. Sie geben uns einen Hinweis darauf, daß man bei Fragen der Teilbarkeit vor allem geometrischen Bezug nehmen kann. Alle ganze Zahlen sind aus Primzahlen aufgebaut. Dividiert man sie beliebig durcheinander, bekommt man rationale Zahlen. Diese machen praktisch den Zahlenstrahl dicht, man könnte gut drauf "stehen". Nur praktisch, wohlgemerkt, denn theoretisch ist er maßlos perforiert: dazwischen liegen Unmengen von irrationalen Zahlen. Ganze Abgründe tun sich auf, es gibt viele Stufen von Irrationalität. Diese Zahlen sind alle Individualisten. Zum Glück gibt es wegen der Bit-Beschränkung diese irren Zahlen im Computer nicht, sonst würden ihm die Lösungen in unendlichen Tiefen verlorengehen. Er würde sich im größten Labyrinth der Welt verirren, sich im Irrationalen herumtreiben und eher träumen als arbeiten.

Aber unsere Geometrie ist tatsächlich so. Es ist der Zusammenhang zwischen Kreisumfang und Radius, zwischen Rechteckseite und Diagonale, betrifft überhaupt alle gebrochenen Potenzen von Primzahlen (z.B. P^(1/3)).

Es geht hier um die Umkehroperation der Dimensionsbildung: Projektion. Wir sind schon wieder beim Kondensieren. Ein Beispiel: In gewissem Sinne ist die Umkehroperation des Vektorproduktes das Skalarprodukt. Das Vektorprodukt geht aus der Ebene zweier Vektoren hinaus in die dritte Dimension, das Skalarprodukt verkürzt die vorhandene ebene Information in eine linienförmige. Beim Projizieren bleibt nur im Symmetriefall das Wesentliche erhalten. Ansonsten sind Kräfte entstanden. Das Vektorprodukt beschreibt oft in der Physik das Abstrahlen von Energie in eine neue Richtung, das Eröffnen einer neuen Dimension, das Gegenteil der Kondensation. Wieder ein Hinweis auf die raumverändernde Wirkung der hochfrequenten Biostrahlung.

Sollen zwei Wellen eine Überlagerungswelle (Schwebung) bilden, müssen sie ein rationales Frequenzverhältnis haben, damit sie irgendwie ineinanderpassen. Jetzt kommt auch wieder der Zusammenhang von Interferenz und Primzahlen. Man trifft die rationalen Frequenzverhältnisse in den periodischen Fenstern des Chaosbandes, als besondere Anfangswerte der jeweiligen Iteration, die zu Interferenzen führen.

GOLDENER SCHNITT

Wie die Blume den Goldenen Schnitt macht

Sehr interessant ist, daß einige Pflanzen ihre Knospen oder Blütenblätter winkelmäßig nach dem Goldenen Schnitt verteilen. Zum Beispiel weist die Lage der Sonnenblumenkerne in der flachen Blüte keinerlei Periodizität auf, ähnlich wie die Facetten im Seepferdchenauge des Apfelmännchens. Die Pflanzenteile werden vermutlich diese extreme Irrationalität als Potentialtrichter oder als Potentialberg ihrer eigenen Hologrammstruktur empfinden und sich genau dort anordnen, wo sie am besten leben können. Entweder liegen die Blütenzentren im lebendigen Schwingungsmaximum, oder es trifft das Gegenteil zu: Bei w₁/w₂=irrational existieren absolut keine Wellen und am allerwenigsten beim Goldenen Schnitt (F). Und genau in diese Täler der ungestörten Ruhe könnte die Pflanze ihre Zentren positionieren. Messungen müßten hier Klarheit bringen. Das Blüten-Hologramm muß solche optimierten Frequenzen tragen, um die Morphologie zu kodieren. Optimaler geht es offenbar nicht. Das Geometrische wird von der Natur voll ausgeschöpft.

Als gesichert gilt zumindest, daß der Verzweigungscharakter bei Pflanzen auf dynamische Wachstumsgesetze zurückzuführen ist, die zweifellos auf der numerischen Fibonacci-Reihe beruhen und genau deshalb im Grenzwert den Goldenen Schnitt ergeben. Die Fibonacci-Reihe hat die Reihenfolge 1,2,3,5,8,13,21,34 usw.. Immer werden die letzten beiden Zahlen addiert, um die nächste zu finden. Die Pflanze schaut von der Gegenwart einen Schritt in die Vergangenheit, um einen Schritt der Zukunft zu bilden. Den Rest der Vergangenheit vergißt sie, und auch den übernächsten Schritt der Zukunft kennt sie noch nicht. Würde sie mehr als drei Generationen im Auge behalten, wäre das harmonische F-Optimum nicht garantiert. Denken wir diesbezüglich nur einmal an unsere Familien!

Kettenbrüche

Irrationale Zahlen, d.h. ihre Anfänge, kann man als Kettenbrüche schreiben. pi wäre demnach pi=3+1/(7+1/(15+1/(1+...))).

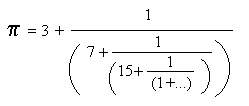
Man kann das auch kompakt aufschreiben pi=(3,7,15,1,...). Je größer diese Ziffern sind, desto eher läßt sich die Zahl durch eine rationale Zahl approximieren. Nach dieser Definition wäre z=(1,1,1,1,1...)

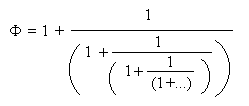
die irrationalste Zahl durch einfache Rekursion, die Zahl mit der schwächsten Konvergenz zur rationalen Näherung. Oder sogar die Zahl g=(0,1,1,1,1...) ? Das ist der Goldene Schnitt, definiert über g=1/(1 + g). Das zweite g wird nochmal durch das erste ersetzt usw., sozusagen die perfekte unendliche Rekursion aus einfachsten Einheiten. Vielleicht ist manchem die andere Darstellung des Goldenen Schnitttes geläufiger: Das Ganze verhält sich zum größeren Teil, wie der größere Teil zum kleineren 1: g = g : ( 1 - g ). Am rechtwinkligen Dreieck davon abgeleitet, erhält man F=1+g=1.6180339=(sqrt(5)+1)/2. Weiteres zum Thema F finden Sie in der ausgezeichneten Arbeit von Hans Jäckel (r&z special 7, S.296, und hier).

Irrationale Zahlen gehören also zu Rekursionen, die nie ein Ende finden. Genauso ist der chaotische Attraktor definiert. Würde eine solche Zahl an beliebiger Stelle in eine Wiederholungs-Sequenz einschwenken, wäre es eine rationale Zahl. Irrationalität und deterministisches Chaos sind identisch, genauso wie Rationalität und Periodizität identisch sind.

Wenn rationale Zahlen multiplikativ miteinander verknüpft werden, kann keine irrationale Zahl entstehen, umgekehrt ja. Wenn z.B. die Wurzel einer Primzahl mit sich selbst multipliziert wird, führt das zu einer rationalen Zahl. Werden aber in beiden Fällen Additionen dazwischengeschaltet, oder gar anschließend Invertierungen oder Divisionen, dann kann als Ergebnis erneut oder erstmals eine irrationale Größe auftauchen, analog den Kettenbrüchen. Auf Rückkopplungsschaltungen in der Elektrotechnik übertragen, müssen gewisse parallel angeordnete und in Reihe angeordnete Bauelemente zusammenwirken (Invertierungen und Additionen), um einen interessanten Attraktor zu erzeugen. Biosysteme sind immer gleichzeitig parallel und in Reihe angeordnet.

Quellen:

Augustin, Peter: Das oberflächliche und wässrige wesen des Lebendigen, erhältlich bei: WERKSTATT FÜR DEZENTRALE ENERGIEFORSCHUNG e.V., Pasewaldtstraße 7, 14169 Berlin
Augustin, Peter; Druschke, Albert R.; Peschel, Manfred: "Vom Wassertropfen zur Peristaltik" , wissenschaft und fortschritt, Berlin 40(1990)12, S.347
Peschel, Manfred: Rechnergestützte Analyse regelungstechnischer Systeme, Akademie-Verlag Berlin 1992

Peschel, Manfred; Breitenecker, Felix: Kreisdynamik . Akademie-Verlag Berlin 1990

Bildunterschriften (in Reihenfolge des Textes):

Bild Kaulquappe Apfelmännchen oder Kaulquappe ?
Bild Wappen ein Krebs? (um 90^o gedreht)
Bild Teufel: Teufel ? Verkopplung(A3) mit k=2 und a=0,5 , (um 90^o gedreht)
Bild 62: Verkopplung (A3) mit k=2 und a=0,17

Programmlistings (Engel und Teufel)

Applet zum Game:   
http://www.2hn.de/game/game152.htm

Weitere Bilder (NEU):

Engel:
http://www.aladin24.de/frakt3/1ma/soul/Engel-7n.jpg

Siehe zum Beispiel ein Java-Applet zu dieser Programmgruppe:
http://www.2hn.de/gamePict/15/152-76993.htm

 
weitere Bilder (Name beginnt mit 152-) auf   http://www.2hn.de/gamePict/bilder2.htm

Fortsetzung Teil 3b

Home Chaos

Home