........................Bild groesser
Chaos,
Biologie und Fraktale
(Veröffentlichung
1996)
Teil 3b
HYPERKOMPLEXES
Die periodischen Attraktoren beschreiben wir im Komplexen Zahlensystem (Gaußebene). Könnten neue hyperkomplexe Zahlensysteme für lebendige Systeme mit "Seltsamen" Attraktoren dieselbe Rolle als einfaches Beschreibungsmittel für chaotische Bewegungen spielen, wie die Komplexen Zahlen für alle bisher bekannten Bewegungen? Die Ansätze 1 bis 3 habe ich mir selbst ausgedacht, weil ich die Gaußebene verallgemeinern wollte, aber am Anfang die sonst üblichen Quaternionen (hyperkomplexe Zahlen) nicht kannte. Mit Quaternionen funktioniert das Ganze nicht, wie ich später merkte. Dadurch, daß bei meinen Ansätzen an manchen Stellen durch Null dividiert werden muß, entstehen Singularitäten, die jedem Mathematiker Angst machen, so daß er solche Ansätze sofort als mathematisch verboten verwirft. Ich als Physiker freute mich am Ergebnis. Die Singularitäten sind punktförmig und rechentechnisch gut beherrschbar. Inzwischen sehen auch meine Mathematiker-Freunde darüber hinweg.
Attraktoren aus dem Hyperkomplexen
Die Existenz chaotischer Attraktoren weist auf Vorgänge hin, die mit Schwingungen verwandt sind, aber im betrachteten Bewegungsraum keine konstante Frequenz (w=0) besitzen. Fast immer sind die Iterationsschritte vor Erreichen eines periodischen Attraktors ebenfalls Bewegungen ohne Frequenz, wobei sich jedoch gerade die spätere Frequenz langsam herausbildet. Deswegen könnte die Bezeichnung "verwandt mit Schwingungen" benutzt werden. Die Tatsache, daß beim deterministischen Chaos in individuellen Schnittebenen des Bewegungsraumes eine charakteristische, oft fraktale Abbildung gefunden werden kann, weist auf eine höherdimensionalere Einbindung hin. Die folgende Methode der Ermittlung nichtlinearer Parameter über unkonventionelle hyperkomplexe Ansätze erzeugt auch sehr lebensnahe Computerbilder.
Jedes Polynom f (Z) = 0 kann durch Iteration mit dem NEWTON-Verfahren
Zn+1 = Zn - f (Zn) / f ‘(Zn) .................(A1)
gelöst werden, auch wenn Z = x + iy eine komplexe Größe ist. Bei Mehrfachlösungen hängt das konkrete Einzugsgebiet (als Farbe im Bild) von der Wahl der Anfangswerte xa und ya ab (Koordinaten des Bildpunktes). Für die drei Fixpunkte der Gleichung
Z3 + 1 = 0 ..........................................(A2)
ergibt sich das bekannte Fraktal, an dessen Linien immer alle drei Gebiete aneinanderstoßen. Nennen wir es den dreizackigen "Einfachstern".

Hyperkomplexe Erweiterung
Setzt man jetzt für Z eine hyperkomplexe Zahl, z.B. der Form
Z
= (x+iy)+j(p+it)+s(k+il) , i2 =-1...............................
=
K0+j* K1+s* K2 ...............................(A3)
ein, und löst (A2) mit (A1) für alle Komponenten von Z, dann ergibt sich mit Ansatz 1 für pa = xa , ta = ya ein sechszackiger "Doppelstern" aus 9 Farben (9 vierdimensionale Lösungen) und analog für Ansatz 2 ein "Dreifachstern" aus 27 Farben, d.h. 27 sechsdimensionale Lösungen. Eine weitere in manchen Bildern realisierte Variante ist Ansatz 3.
 Ansatz 1, reines Newtonverfahren |
|
Ansatz 1:
(A3)......... mit j2 = - i , s = 0 , wobei
Z = K0 - j * K1
Z * Z = K02 + i * K12
Ansatz 2:
(A3)......... mit j3 = - i , j2 = s , wobei
Z = ( K02 + i * K1 * K2 ) + j ( -i * K22 - K0 * K1 ) + s ( K12 - K0 * K2 )
Z * Z = ( K03 - K23) + i (3 * K0 * K1 * K2 - K13 )
Ansatz 3:
(A3)........ mit j2 = - 1 - i , s2 = 1 + i , js = - sj = 1-i
Rückprojektion durch Einschränkung der Freiheitsgrade
Wenn nun Gleichung (A1) in verstümmelter Form benutzt wird, indem man die Iteration einer oder mehrerer Variablen unterläßt, sie wie Konstanten festhält, entfernt man sich vom ehemaligen f(Z). Man bearbeitet für jeden Bildpunkt nun eine zwar benachbarte, aber neue nichtlineare Gleichung, die im allgemeinen nicht mehr analytisch darstellbar ist. Das vorher durch (A1) abgeschlossene (konservative, optimale) System des "Sterns" wird geöffnet, erhält Restriktionen durch das Nullsetzen oder Verändern von dp und dt. Die Zahl der Freiheitsgrade, die vorher durch den hyperkomplexen Ansatz erhöht wurde, wird nun über eine Rückprojektion wieder eingeschränkt, wiederum wie bei Kondensation. Jeder Eingriff in (A1), wie
pn+1 <> pn - dp ...................................(A4)
muß als Verlust bzw. Zuwachs bezeichnet werden, vergleichbar mit Dissipation.
Es entstehen Bilder neuartiger Struktur (siehe oben und Bilder Ansatz 1 u.2 ). Für p und t um +-2 endet das Gebilde, während der Stern (keine Störung des Optimums) bis Unendlich reicht. In der Nähe des Bildmittelpunktes, bei sehr kleinen p,t-Werten, entsteht der Einfachstern. Je mehr man nach außen wandert, desto "verbeulter" werden seine Glieder.
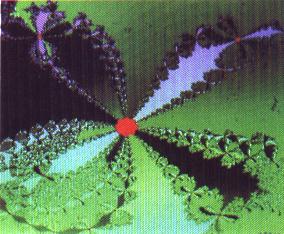
Dann entstehen sprunghaft völlig neue Fraktale. Die alten Fixpunkte sind verschwunden, neue erschienen, und die Gebiete mit zyklischen Lösungen erinnern an "Wirbelsäulen" und "Insektenflügel". "Kakteenkugeln" mit blumiger Feinstruktur tauchen auf. Durch eine entsprechende Farbkodierung lassen sich somit Welten darstellen, die der lebendigen Welt nicht unähnlich sind. Bei den Bildern mit einer leeren Mitte wurden alle Anfangswerte von x und y mit einer ausgewählten Systemlösung (x,y) von p = t = 0 belegt. Hier Bilder Ansatz3 vom Amiga-Bildschirm .
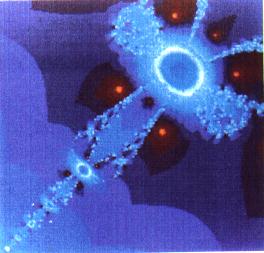
Doppelstern mit p=p-dp/6, t=t-dt/6, brx=bry=1, vsx=vsy=-0.8888
Da die blumigen Schleifen, Flügel und Netze mit allen drei Ansätzen entstehen, sind solche fraktalen Formen offenbar schon spezifisch für diese Methode. Für Z5 + 1 = 0 usw. erhält man analoge Muster, natürlich mit 5-zähliger Symmetrie:
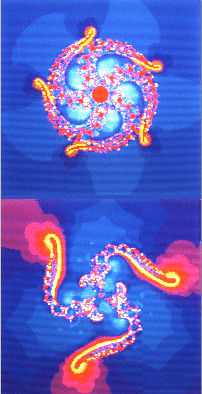
Das Interessante hier ist, daß die mathematischen Restriktionen als Kräfte zu verstehen sind, die auf das System einwirken. Das ungestörte Optimal-System des "Stern" ist selbstähnlich ohne Ende in Raum (und Zeit! ). Und irgendwie doch langweilig trotz aller Harmonie. Wie ist das so im Leben? Kräfte, die wir schon durch die eigene Masse erleben, drängen uns aus dem Optimum, aus dem Gleichgeweicht. Wir leben in der Polarität zwischen Yin und Yang, Mutter und Vater, hell und dunkel, gut und böse usw. . Wir atmen aus und ein. Wir müssen geben und nehmen. Und das häufig unter dem unbewußten Ahnen der Wirklichkeit: Dem Zurück-Sehnen zum Ursprung, zur kräftefreien Harmonie, aus der wir freiwillig herkamen, um die bestimmt nicht langweilige Polarität zu erleben.
Gleichgewicht und Nichtgleichgewicht
Iteriert man (A1) mit (A2) ohne (A4), also unter vollständiger Einbindung in ein höheres System, dann entspricht das Ganze einem statischen Gleichgewicht. Bifurkationen treten nicht auf. Man "sieht" dieses Gleichgewicht förmlich den "Sternen" an und auch den Lösungen:
Die neun vierdimensionalen Lösungen für Ansatz 1 liegen symmetrisch zur Null. Jeweils drei benachbarte bilden ein gleichseitiges Dreieck. Aber alle drei Dreiecke haben zueinander gleiche vierdimensionale Abstände. Man könnte sich je zwei der Dreiecke als die Dach-Giebelseiten eines Hauses mit Spitzdach vorstellen. Wenn man drei dieser Häuser so anordnet, daß sich in der Mitte ein geschlossener dreieckiger Innenhof bildet, müßten von den sechs Giebelflächen jeweils zwei miteinander verschmelzen. Ohne Kürzung von Verbindungswänden paßt dieses Gebilde leider nicht in den dreidimensionalen Raum. Es ergibt eine "Unmögliche Figur".
Ein Festhalten oder Verändern von Variablen (A4), die vom Newton-Verfahren ihre nächste optimale Korrektur "zur Lösung hin" erhalten könnten, sich aber nicht dorthin bewegen dürfen, ist eine zusätzliche Kraft, die das Gleichgewicht stört, eine nichtlineare Störung. Das System kommt zwangsweise ins Nichtgleichgewicht und versucht trotzdem, den alten Lösungen so nahe wie möglich zu sein. Es wurde nur dp=0 gesetzt, nicht p, so daß weder die alten komplexen, noch die "richtigen" hyperkomplexen Lösungen erreicht werden können. Wie eine undurchdringliche Wand steht "p= const" dazwischen. Die "Wand" kann auch als ständige Absorption oder Emmission gesehen werden, die das System verkraften muß. Also bewegen sich die restlichen freien Variablen irgendwo dazwischen und finden neue, diesmal meist dynamische Gleichgewichte. Wenn (A4) zeitvariabel wäre, hätte die Dynamik alle Züge des Lebendigen. Was beim Apfelmännchen Zn+1=Zn2+C der nichtlineare Parameter C war, wurde hier aus dem Hyperkomplexen "künstlich geboren" , nämlich p= const und t= const.
Wie bei der Modulo-Funktion das Ergebnis im Modulo-Kasten bleiben muß (s.Teil 5), wurde hier die Variable im Projektionskasten p=const, t=const festgehalten. Durch das Verbiegen der Trajektorien von p und t müssen x und y bifurkieren. Um es noch anschaulicher zu sagen: Es wirkt ein zu (A1) und (A2) als dritten Einfluß zu bezeichnenedes "Kraftfeld", das durch (A4) das dp und das dt gegen Null drückt.
Die bifurkierende Nichtlinearität stellt sich erst durch das Zusammenwirken von mindestens drei Komponenten ein, was sich schon an der komplizierten Dynamik des Dreikörperproblems zeigt, im Gegensatz zum beherrschbaren (leider nicht existenten) Zweikörperproblem.
Eigenschwingungen von beweglichen Systemen entstehen, wenn eine Kraft auf sie eingewirkt hat. Damit ist klar, daß man neue Frequenzen entweder aus anderen additiv aufbaut (kommensurabel) oder neu erzeugt durch einen Anstoß und Rückkopplung aller Systembestandteile. Für beides wäre, neben der komplexen, eine hyperkomplexe Wellenbeschreibung geeignet. Diese würde eine "innere Dissipation" zulassen, d.h. eine Rückkopplung zwischen den komplexen Komponentenwellen untereinander. Die Art der Rückkopplung kann in der mathematischen Form des hyperkomplexen Ansatzes vorgegeben werden, der vielleicht für konkrete Anwendungen offen zu bleiben hat. (Es könnte aber auch DEN ANSATZ geben (universell gültig), mit dem die ganze Welt dupliziert werden kann.) Sollte die Dissipationsenergie auf diese Weise einen geschlossenen Weg durchlaufen, dann tritt sie nach außen nicht in Erscheinung. Die Fourierzerlegung einer solchen Welle kann den tatsächlichen Vorgang nicht erfassen.
Siehe
zum Beispiel ein Java-Applet zu dieser Programmgruppe:
http://www.2hn.de/gamePict/20/203-23763.htm
weitere Bilder (Name beginnt mit 203-) auf http://www.2hn.de/gamePict/bilder3.htm
Oder
Applet:
http://www.2hn.de/gamePict/20/205-75635.htm
weitere Bilder
(Name beginnt mit 205-) auf http://www.2hn.de/gamePict/bilder4.htm