Hier erstmal zur Wiederholung das bekannte Apfelmännchen von Benoit Mandelbrodt:

Apfelmännchen
(Bildbreite 8),
links: Divergenz bunt kodiert, rechts: Zahl der Iterationen als Farbe
etwas größer
Anfangswerte pro Punkt: x=0: y=0
Schleife für Bildachsen Cx (horizontal), Cy(vertikal):
x1 = x*x-y*y+Cx
y1 = 2*x*y+Cy
x=x1: y=y1
Was wäre
wenn
das
Apfelmännchen (Z=Z*Z+C mit Z und C komplex)
nur ein nettes
kleines Monster wäre ?
Es könnte der verzerrte Schatten einer
vektoriellen 3D-Verkopplung (P,E,H,C Vektoren)
P=ExH+Cx E=HxP+Cy H=PxE+Cz
sein, die
wirkliche physikalische Bedeutung hat,
da wäre das sinnlose Addieren
von Fläche und Strecke vorbei.
C hätte die Bedeutung eines Vektorfeldes
bestimmter Richtung und Größe.
Das Ganze wird nun ein Turbulenzenbild
für Strömungen
Wir müssen weiterrechnen,
bis die Gleichung den Tragflügel erzeugt.
Doch zuerst kam ein UFO.
Folgende
Bilder entstanden aus der wiederholten
Anwendung folgender Schleife
|
Px=Pxn: Py=Pyn: Pz=Pzn Pxn=(Ey*Hz-Ez*Hy)+Cx |
Bild am Seitenanfang: Cz=1.0 |
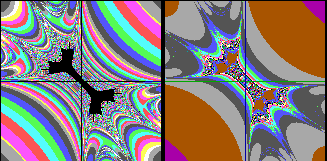 Cz=konst=0.6 (Bildbreite 8), Bildkoordinaten Cx und Cy |
|
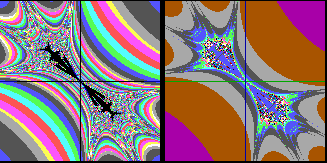 Cz=1.6 (Bildbreite 8) |
|
Der Mandelbrotmenge
entspräche ein Kugelzentralfeld wachsender Größe, was realen
Zentralfeldern widerspricht. Es müßte vom Betrag her eher invers
sein ( C_neu=1/C ).
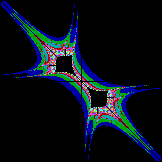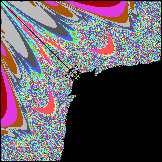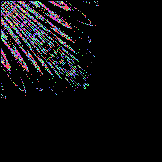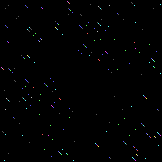
Hier Bildquadrant oben links mit inversem C für Bildbreite
200 und Cz=konst=0.6, daneben ein Detail daraus, darunter alle 4 Quadranten
für Bildbreite 8 (gleiche Rechnung, das rechte Bild zeigt jeweils die Anzahl
der Iterationen). Ganz unten als Vergleich das Apfelmännchen mit inversem
C, auch Bildbreite 8.
 .
.

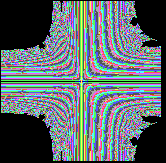
Zum Vergleich inverses Apfelmännchen
Cx-->1/Cx
Cy-->1/Cy
Punktweise Kreuzprodukte bilden sich aus 2 Vektorfeldern, eins ist ein konstantes
Vektorfeld (z.B.Geschwindigkeit v oder Frequenz f ), das andere ist ein Gradientenfeld
(dv/dt).
Heraus kommt ein Vektorfeld, das senkrecht auf den beiden ersten steht. Wann
"geschieht" dies ? Gleich so, von selbst ? Oder was muß noch
hinzukommen ?
In den Einzelteilen des Apfelmännchens (ohne Addition von C) haben wir zwei sich kreuzende Hyperbelscharen, sie drücken jeweils die Funktion 1/x aus (für Realteil gedreht um 45Grad):
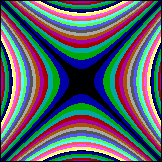 f(x,y) = (x*x - y*y) mod 15 |
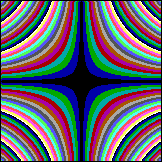 f(x,y) = (2*x*y) mod 15 |
Und wenn das "wahre" Apfelmännchen aus vektoriellem Kreuzprodukt und Vektor-Addition besteht, statt aus Komplexer Quadrierung und Addition, dann sollte in ebendieser neuen Gleichung auch die Inversion (d.h. die Hyperbel) versteckt sein.
Eine plausible Lösung findet man auf
http://www.aladin24.de/chaos/chaos5a.htm
Gemäß den Gleichungen (A1) bis (A4) erzeugt man Bild1
mit der zeilenweisen Abbildung von Cosinuswellen (hier von links nach rechts
die AusbreitungsRichtung der Wellen) mir dem zeilenweisen Ansteigen der Frequenz
automatisch auch das 2. Vektorfeld (von unten nach oben als Frequenzgradient).
Wenn der Gradient "sauber laminar" ist, entstehen als VerbindungsLinien
aller äquivalenten Schwingungsknoten automatisch die 1/x -Hyperbeln, genau
wie hier bei f(x,y), wenn man die Hyperbeln direkt ausrechnet.
Analogon:
In elektrischen Schaltungen werden Widerstände und Induktivitäten
ebenso entweder direkt oder als Inversgrößen addiert, je nach Reihen-
oder Parallelschaltung (in Reihe und parallel ist auch um 90 Grad verschieden).
Auch Brennweiten von optischen Linsen werden invers addiert, wenn man sie nacheinander
schaltet, wie bei der Addition von Kapazitäten. Der Gradient zu einem Fluß
(der Fluß ist zeitliche in Reihe/Nacheinander) ist dasselbe wie eine Parallelschaltung
(zeitlich parallel/gleichzeitig).
Das Ganze hängt auch mit der Exponentialdarstellung der Komplexen Zahlen zusammen. Befindet man sich im Bezugssystem des Argumentes y der Funktion A=exp(iy) (also in einem rotierenden System bei Phase y), dann gilt als Umkehrfunktion y=ln(A) . Von diesem die erste Ableitung (Gradient senkrecht dazu) ist die Funktion y'=1/A . Das Gravitationspotential oder das Coulombpotential haben auch radial den abnehmenden Verlauf 1/r (Zentralpotential).
Das Ideale am Zentralpotential (Beispiel Kugelwelle aus Strahlungsquelle) ist,
daß die Äquipotentialpunkte auf den zentrischen Kreisen(Kugeln) die
Bedeutung einer Parallelschaltung einnehmen (Gleichzeitigkeit), während
die radial nach außen gerichteten Punkte zeitlich nacheinander (in Reihe)
ankommen. Das Strömen nach außen (weg vom Mittelpunkt) ist ein Fluß,
dessen seitlicher Gradient bei jedem r abnimmt. So sind schon zwei Vektorfelder
vorhanden, ohne etwa eine Randbedingung wie beim Fließen von Wasser in
einer Röhre (Reibung an Wand).
Es kommt dann automatisch zu Turbulenzen innerhalb der Kugelschalen (z.B. Sonnenflecken),
und es müssen sich auch globale Kreisflüsse einstellen, die am Ende
eine Eigenrotation der Quelle erzeugen. Dann gibt es noch eine Rotationsachse
mehr, die komplexere Verkopplungen (Kreuzprodukte) zur Folge hat.
Die Kreuzprodukte sind nicht weniger "Komplex", obwohl sie kein i*i=-1 brauchen: Senkrechtstehende Vektoren bringen das Maximum an Fluß, genau wie Parallelschaltung aller Widerstände,(d.h. senkrecht zum Fluß geschaltet/betrachtet). In kartesischen Koordinaten sind die Grundvektorsysteme zu sich selbst reziprok.
Multiplikationstabelle:
|
|
i
|
j
|
k
|
|
i
|
0
|
k
|
-j
|
|
j
|
-k
|
0
|
i
|
|
k
|
j
|
-i
|
0
|
Jetzt kommt das Beste (bzgl.Thema auf chaos5a.htm): Wenn man dem ganzen Bild (mit gleichmäßig gekrümmtem Gradienten) ein zweites Raster aufaddiert, so, wie man es bei Juliamengen mit der Addition von C macht (gleiche Größe C an jedem Punkt), ergeben sich neue Strukturen, die eindeutig an Wirbel erinnern. Diese Wirbel haben ihre Drehachsen senkrecht zur Bildebene. Die Anzahl k der Wirbel pro Achsenrichtung berechnet sich aus Gleichung (A6):
|
|
| G | ist die Zahl der Zeilen oder Spalten des Bildes in betrachteter Achsrichtung(Addiertes Raster). |
| m | ist der Modulo-Wert der Linienstruktur, mit dem die Farben kodiert sind (z.B. color = (x*y) mod 15 für m=15 Farben). |
| d | ist die Gesamt-Bildbreite bzw. Bildhöhe in x oder in y-Koordinaten (pos. und negative Richtung zusammen) für die Linienstruktur, wie Hyperbeln oder Ellipsen etc.. |
Für k=1 und nach (A6) berechnetem d ergibt sich das Symmetriebild, bei dem die mittleren Frequenz der Wellenlinien symmetrisch vom Zusatzraster getroffen wird. Es ist auch das Bild mit exakter 1/x-Anordnung der Schwingungsknoten bei richtig dimensioniertem Parameter d. Das Ganze funktioniert nicht nur mit Hyperbeln (2xy) oder (xx-yy), sondern auch mit Kreisen (xx+yy).
Frage: Was bedeutet die Entstehung von Strukturen mit Achsen senkrecht zur Bildebene, obwohl garnichts multipliziert wurde, das als Kreuzprodukt gewertet werden kann? Es wurde im Gegenteil ein zweites Raster ADDIERT auf eine saubere ungestörte Gradientenströmung.
Antwort: Ein Hologramm kann auch erst wiederentstehen, wenn die Referenzwelle
(Raster) hinzukommt. Sie dekodiert das (noch tote) Informationsmuster und gibt
ihm Leben. Genauso ist es beim PC: Die eingeschaltete Taktfrequenz des Computers
und die Hardware zusammen entsprechen der Referenzwelle und erst dann wird die
aufgerufene Information (Software) identisch in Aktion gebracht, wie auf dem
PC des Softwarentwicklers.
Wenn Fluß A und senkrecht dazu dA/dt mit Markierungen (wie Wellenknoten)
die Formen von Hyperbeln oder Kreisen ergeben, ist eine Voraussetzung für
das Kreuzprodukt realisiert worden, allein durch die Ordnung im Gradienten.
Das heißt im Klartext: Die ungestörte Gradientenströmung bietet
durch die verschieden ausgerichteten Komponenten "Strömung" und
"Gradient" zwei Vektorfelder an, die auf eine Verkopplung warten.
Die saubere Addition eines dritten Vektorfeldes (Rasters) erzeugt erst einen
Interferenz-Effekt, vergleichbar mit den Feigenbaumstrukturen, wobei dort die
Rastergröße als Nichtlinearer Parameter fungiert.
|
Hypothese 1: Möglicherweise
sind alle zeitlich stabilen physikalischen Kreuzprodukte nur die Zentren
von Vektorfeldern, die mit solch einer einheitlichen (deshalb noch nicht
registrierten) Raster-Addition verbunden sind, die zur Fixpunktlösung
führt.
|
Die Definition des Kreuzproduktes am Einzelpunkt ist sozusagen auf die Einfachlösung beschränkt und berücksichtigt nie das Einschwingverhalten. Trotzdem kann es einen fließenden Übergang zu Mehrfachlösungen des "Kreuzprodukt-Feldes" geben, den wir noch nicht als Solchen erkannt haben. Und zeitlich-dynamisch betrachtet gibt es eine weitere Hypothese, wie bereits am Anfang formuliert:
| Hypothese 2: Alle stabilen realen Kreuzprodukte sind dynamisch erzeugt durch rekursive Abfolge ihrer zyklischen Vertauschungen, wobei zusätzlich mindestens in einer Komponente ein stützendes Verkopplungsfeld addiert werden muß, weil es real keine vollkommene Perfektion (bezüglich orthogonaler Vorgänge ohne Störung) gibt. |
Autorin: Gabi Müller