Diskus
 |
|
 |
|
 |
|
 |
|
 |
|
|
Zum Vergleich
neuere Rechnungen als Java-Applet:
|
|
|
Programm: innere Schleife pro Bildpunkt: Px=Pxn: Py=Pyn: Pz=Pzn Pxn=(Ey*Hz-Ez*Hy)+Cx Exn=(Hy*Pz-Hz*Py)+Cx*my Hxn=(Py*Ez-Pz*Ey)+Cx*my x=Pxn: y=Pyn: z=Pzn |
Bilddaten Bildbreiten Mittelpunkt: my=-0.5 Cx=x-Achse für r=sqr(x^2+y^2+z^2) |
 |
|
|
hier rechte Seite: vsx=0.818 (anderes Vorzeichen an vsx wie oben)
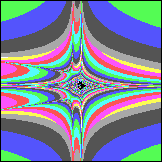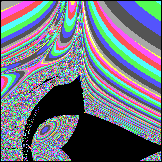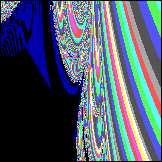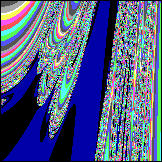
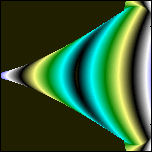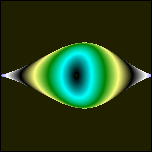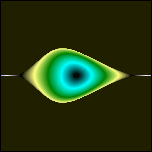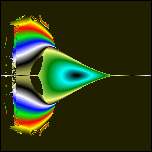
Vorläufige Auswertung: Die wellenförmigen Gebilde um den Diskus erinnern an Auraschichten. Sie sind Abbild der Liniendichte um den Diskus herum, entstehen wahrscheinlich erst mit dem Bildschirmraster zusammen, weil es so dünne Linien sind, daß sie mit Pixeln nicht mehr gezeichnet werden können. Nur Teile der dünnen Linien treten hervor und suggereieren mit anderen Zeilen zusammen Wellen, die außen am Diskus hoch (an Oberseite, bzw. Unterseite runter) zu den beiden Polen fließen. Durch das negative my sind 2 entgegensetzte Strömungen definiert worden, in denen sich die rekursiven Kreuzprodukte immer im Kreise "abspulen". Einige ihrer Komponenten haben in jeder Schleife Strömung A zu addieren: Cx, Cy, Cz und andere haben Strömung B zu addieren: -0.5*Cx, -0.5*Cy, -0.5*Cz. Die Strömung B wird insgesamt zweimal eingesetzt, deswegen reicht der Wert my=-0.5 für die Kompensation von Strömung A. [ Der Faktor +1/2 taucht an einigen Stellen der Physik auf (Nullpunktseenergie etc.), möglicherweise zeigt das nur eine ähnliche unvollständige Kompensation an, wie hier. Die Strömung ist in Wirklichkeit doppelt, wir sehen also nur die Hälfte, weil wir nur die Projektion kennen, also eine Dimension "vergessen".] Der schwarze Diskus innen zeigt alle konvergenten Lösungen. Soweit ist alles wie beim Apfelmännchen. Von fraktaler Oberfläche, wie beim Apfelmännchen, ist nichts zu erkennen, was sich aber bei anderen my etwas ändert (hier my=1/3):
Zu den Diskusgrößen: halbe Höhe: vsy=0.32838 (ist bei
Bildbreite bry=0.0001 noch in der Mitte). Damit ist die gesamte Höhe
gleich 0.65676, was in der Nähe des Goldenen Schnittes g
liegt, denn die Diskusbreite liegt etwa bei der inversen Größe,
nämlich 1.6 bis 1.5 (er ist nicht scharf abgegrenzt). Dieses inverse
Verhalten ist verdächtig, denn beim Goldenen Schnitt gilt: fi=1/g,
g=fi-1, fi+1=fi*fi Es gibt eine zweite Parameterkombination, die einen Diskus liefert:
Siehe dazu oben den Programmteil , wobei |
|